Bottom-Up Parsing

class: center, middle

# Bottom-Up Parsing

_CMPU 331 - Compilers_

---

# Bottom-Up Parsing

* Bottom-up parsing is more general than top-down parsing, but just as efficient

* Builds on ideas in top-down parsing

* Bottom-up parsers don't need left-factored grammars

* Bottom-up is generally preferred

---

# Introductory Example

Grammar:

```
    E → T + E | T
    T → id * E | id | (E)
```

String:

```
    id * id + id
```

---

# The General Idea

Remember that top-down parsing begins with the _start symbol_ (the top of the tree), and replaces each non-terminal with the right-hand side of some production.

```
    E → T + E | T
    T → id * T | id | (E)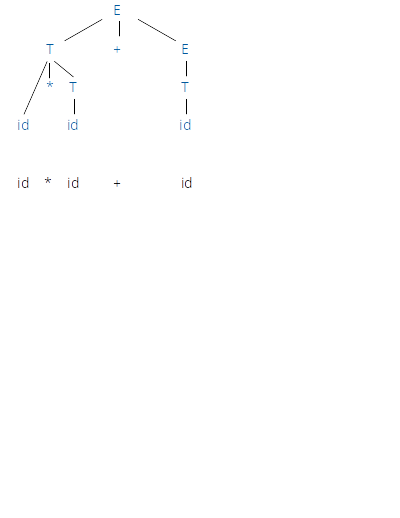
```

![bottomup](/~cs331/images/lectures/bottomup.png)

---

# The General Idea

Remember that top-down parsing begins with the _start symbol_ (the top of the tree), and replaces each non-terminal with the right-hand side of some production.

```
    E → T + E | T
    T → id * T | id | (E)
```
Left-most derivation:

```
    1. E                     E → T + E
    2. T + E                 T → id * T
    3. id * T + E            T → id
    4. id * id + E           E → T
    5. id * id + T           T → id
    6. id * id + id
```

---

# The General Idea

Bottom-up parsing starts with the source, and _reduces_ it by applying productions in reverse, until it reaches the start symbol.

```
    E → T + E | T
    T → id * T | id | (E)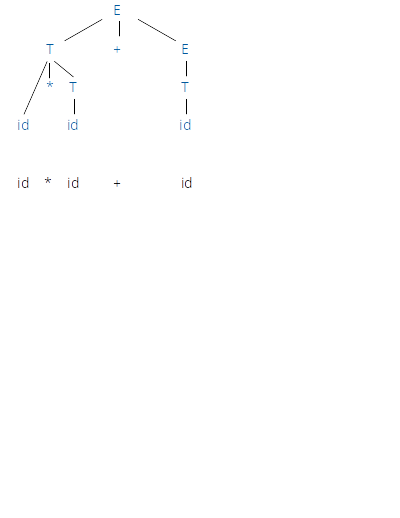
```

![bottomup](/~cs331/images/lectures/bottomup.png)

---

# The General Idea

Bottom-up parsing starts with the source, and _reduces_ it by applying productions in reverse, until it reaches the start symbol.

```
    E → T + E | T
    T → id * T | id | (E)
```

```
    1. id * id + id          T → id
    2. id * T + id           T → id * T
    3. T + id                T → id
    4. T + T                 E → T
    5. T + E                 E → T + E
    6. E

```

---

# Important Fact

A bottom-up parser traces a right-most derivation in reverse

---

# Different Kinds of Parsers

LR(k) grammars

* "L" means "left-to-right" scan of input
* "R" means "right-most derivation"
* The "k" says how many tokens it looks ahead

LR(1) parsers lookahead by one token

---

# First Attempt Algorithm

Informal description:

```
   I is the input string
       repeat until I == E (start symbol) or run out of possibilities
           pick a non-empty substring S of I
           if we have a production X → S
               replace one S by X in I
           else if no such production, backtrack
```

* Not very fast

* Doesn't handle all cases

* How do we choose which substring to reduce at each step?

---

# Shift-Reduce Parsing

* Split input string into two substrings
  * Right substring is not yet examined by parsing (a string of terminals)
  * Left substring has terminals and non-terminals

* Notation: dividing point is marked by | (which is not part of the string)

* Initially, all input is unexamined, so | is at the start of the string (far left, for left-to-right)

```
    |abc
```

* Only two kinds of actions: _shift_ and _reduce_

---

# Shift

Move | one place to the right

```
    ABC|xyz
    ABCx|yz
```

* We say the action _shifts_ the terminal `x` to the left substring

---

# Reduce

Apply a production in reverse at the end of the left substring

* If `D → xy` is a production, then:

```
    ABCxy|z
    ABCD|yz
```

---

# Example

```
    E → T + E | T
    T → id * T | id | (E)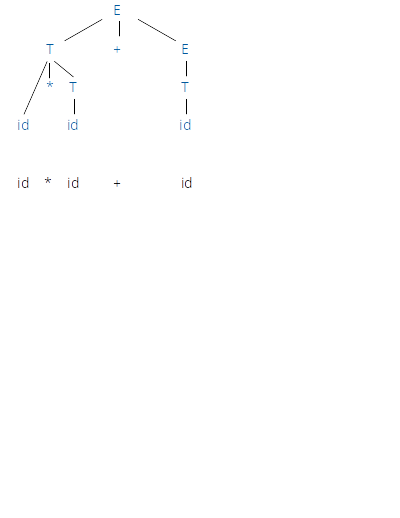
```

![bottomup](/~cs331/images/lectures/bottomup.png)

---

# Example

```
    E → T + E | T
    T → id * T | id | (E)
```

* Shift: move | one place to the right
* Reduce: apply a production in reverse at the end of the left substring

---

# Using a Stack

* Left substring can be implemented by a stack
  * Top of the stack is at the |

* Shift pushes a terminal on the stack

* Reduce pops zero or more symbols off the stack (right side of a production) and pushes a non-terminal on the stack (left side of a production)

---

# Conflicts

* In a given state, more than one action may lead to a valid parse

* If it is legal to shift or reduce, there is a _shift-reduce_ conflict

* If it is legal to reduce by two different productions, there is a _reduce-reduce_ conflict

---

# Key Issue

How do we decide when to shift or reduce?

```
    E → T + E | T
    T → id * T | id | (E)
```

* At step (2) of the example:

```
    2. id | * id + id          shift
    3. id * | id + id          shift
    4. id * id | + id          ...
```

* We could have decided to reduce instead:

```
    2. id | * id + id          reduce T → id
    3. T | * id + id           ...
```

* Would be a mistake, there is no way to reduce to start symbol E

---

# Handles

* A handle is a string that can be reduced and also allows further reductions to the start symbol

* Tied to a particular production at a particular position

* If we have a string `abc`, then the production `X → b` in the position after `a` is a _handle_ of `abc`

* We only want to reduce at handles

---

# Handles

* In shift-reduce parsing, handles always appear at the top of the stack

* Handles are never to the left of the right-most non-terminal
  * This means shift-reduce moves are sufficient
  * The | never moves backward, only forward in a left-to-right scan

* Shift-reduce algorithms are based on recognizing handles

---

# Recognizing Handles

* No known efficient algorithms to recognize handles

* Solution: use heuristics to guess which stacks are handles

* On some CFGs, the heuristics always guess correctly

---

# Viable Prefixes

* Look for prefixes of the handle

* A prefix is viable, if it is part of a valid state of the shift-reduce parser
  * For our example string `abc`, the `a` is a _viable prefix_ for the _handle_ `X → b` (the production) in the position after `a`

* As long as a parser has viable prefixes on the stack, no parsing error has been detected

* The set of viable prefixes is a regular language, so we can construct automata to that accept viable prefixes

---

# Example

Grammar:
```
    E → T + E | T
    T → id * T | id | (E)
```

String:
```
    (id)
```

* If `(E|)` is a state of a shift-reduce parse

* `(E` is a prefix of `T → (E)`

* An item `T → (E.)` says that we have seen `(E` so far, and hope to see `)`

* After we shift `)`, and move to a state `(E)|` then we can reduce `T → (E)`

---

# Shift-Reduce Parsing

* Construct a DFA (deterministic finite automaton) to recognize all viable prefixes

* An item `I` is valid for a viable prefix `a` if the DFA recognizing viable prefixes terminates on input `a` in a state `s` containing `I`

* The items in `s` describe what the top of the item stack might be after reading input `a`

---

# LR(0) Parsing

* Assume
  * stack contains `a`
  * next input is `t`
  * DFA on input `a` terminates in state `s`
* Reduce by `X → b` if
  * `s` contains item `X → b`
* Shift if
  * `s` contains item `X → b.tw`
  * equivalent to saying state `s` has a transition labeled `t`

---

# SLR Parsing

* Assume
  * stack contains `a`
  * next input is `t`
  * DFA on input `a` terminates in state `s`
* Reduce by `X → b` if
  * `s` contains item `X → b`
  * `t` is an element of the follow set of X
* Shift if
  * `s` contains item `X → b.tw`
  * equivalent to saying state `s` has a transition labeled `t`

---

# LR(0) vs SLR

* LR(0) has conflicts when any state has:
  * two reduce items (reduce-reduce conflict)
  * a reduce item and a shift item (shift-reduce conflict)

* SLR improves on LR(0) shift-reduce heuristics

* SLR grammars are those where the heuristics exactly detect the handles, so no states have conflicts