Type Checking

class: center, middle

# Semantic Analysis: Type Checking

_CMPU 331 - Compilers_

---

# Recap: Stages of Compilation

1. Lexical Analysis
2. Parsing
3. Semantic Analysis
4. Optimization
5. Code Generation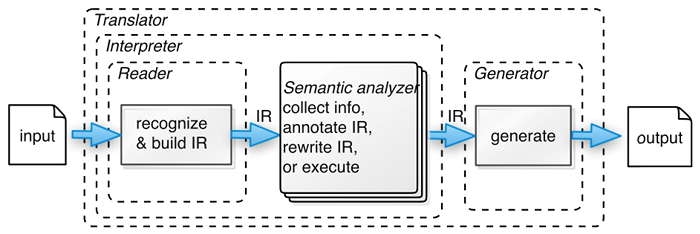

![multistage pipeline](/~cs331/images/lectures/multistage.png)

(source: _Language Implementation Patterns_ by Terence Parr)

---

# Recap: Semantic Analysis

Many possible kinds of checks:

* Identifiers are declared before use
* Types
* Reserved identifiers (keywords) are not misused
* Functions defined only once
* Classes defined only once
* Methods in a class defined only once
* Inheritance relationships
* And others...

The requirements depend on the language

---

# Types

* What is a type?
  * Exact definition varies between languages

* Vague generalization:
  * Set of values
  * Set of operations allowed on those values

---

# Types - Examples

* `int`
  * set of all integer values (generally limited to some finite storage size)
  * operations: + - * /
* `float`
  * set of all real number values (generally limited to some finite storage size, infinite repeating decimals like π = 3.14159265... may be truncated)
  * operations: + - * /
* `bool`
  * set of all boolean values (true or false)
  * operations: `not`, `and`, `or`
* `char`
  * set of all single character values ('a', 'b',...)
  * operations: ==, !=
* `string`
   * set of all multiple character values ("hello world"), may be stored as an array or other data structure
   * operations: concatenation, substring, split

---

# Type Systems

* The type system of a language specifies which operations are valid for which types

* The goal of type checking is to ensure that operations are used with the correct types

---

# Type Checking

Three kinds of languages:

* _Statically typed_: All (or almost all) checking of types is done as part of compilation (C, Java)

* _Dynamically typed_: Almost all checking of types is done as part of program execution (Scheme, Python)

* _Untyped_: No type checking (machine code)

---

# The Type Wars

* Competing views on static vs. dynamic typing

* Static typing fans say:
  * Static checking catches type-related programming errors at compile time
  * Checking types at compile time (once) avoids overhead of runtime checks (many times)

* Dynamic typing fans say:
  * Static type systems are weirdly restrictive (sometimes it makes sense to add an `int` and a `float`, check the boolean truth of an `int`, or concatenate an `int` to a `string`)
  * Programmer time is expensive, computer time is cheap, and programmers waste a lot of time working around static type systems
  * Interpreted languages (like Python) recompile every time you run the code, so there is no performance advantage to running type checks at compile time instead of runtime

---

# The Type Wars

In practice:

* Statically typed languages usually have an escape mechanism
  * Type casts in C or Java
  * A Java object has both a static and a dynamic type (a variable could be declared as `Dog` type, but actually hold a `Husky` type object)

* Dynamically typed languages have rules for conversion
  * `int` in boolean context is false if 0, true otherwise
  * `string` in boolean context is false if "", true otherwise
  * if you multiply a `float` by an `int`, it returns a `float`

* Some dynamically typed languages have (optional) type declarations, checked at compile time
  * Gradual typing combines both static and dynamic type checking

---

# The Type Wars

* Don't get sucked into the type wars

* Choose the language that makes the most sense for:
  * the particular problem you are trying to solve, and
  * the particular solution you are trying to implement

* Types are just another way of looking for mistakes in the source code

---

# Type Checking

* The user declares types for identifiers

* The compiler infers types for expressions

* _Type inference_ is the process of filling in type information
  * the type is explicit in the declaration, but not later use
  * the type of the expression `x + y` depends on the types of `x` and `y`

* _Type checking_ is the process of verifying fully typed programs (once you know the types of all declarations and all expressions)

---

# Rules of Inference

* We've seen two examples of formal notation specifying parts of a compiler
  * Regular expressions (lexer)
  * Context-free grammars (parser)

* The formalism for type checking is logical rules of inference

---

# Why Rules of Inference?

* Inference rules have the form
> _If Hypothesis is true, then Conclusion is true_

* Type checking computes via reasoning
> _If E1 and E2 have certain types, then E3 has a certain type_

* Rules of inference are a compact notation for _if-then_ statements

---

# Rules of Inference

The notation is easy to read with practice:

* x: T means "x has type T"
* ⊢ means "it is provable that..."
* Rules have the form:
<center>
⊢ Hypothesis1 ... ⊢ Hypothesis2 
⊢ Conclusion
</center>

Example:
> If E1 and E2 have type `int`, then E1 + E2 has type `int`

---

# Rules for Constants

Integers:

<center>
i is an integer constant 
⊢ i: int
</center>

Booleans:

<center>
b is a boolean constant 
⊢ b: bool
</center>

---

# Rules of Inference

* The inference rules are templates describing how to infer types

* By combining the templates, we can produce complete typings

<center>
<div style="display: table; border-bottom: 1px solid">
 <div style="display: table-row">
 <div style="display: table-cell">
 <center>
 1 is an integer constant 
 ⊢ 1: int
 </center>
 </div>
 <div style="display: table-cell">
 &nbsp;&nbsp;&nbsp;&nbsp;
 </div>
 <div style="display: table-cell">
 <center>
 2 is an integer constant 
 ⊢ 2: int
 </center>
 </div>
 </div>
</div>
⊢ 1 + 2: int
</center>

---

# Type Checking Proofs

* Type checking proves facts, like E: T
  * Proof is on the structure of the AST
  * Proof has the shape of the AST
  * One type rule is used for each AST node
* In the type rule for a node E:
  * Hypotheses are the proofs of types for subexpressions of node E
  * Conclusion is the type of node E
* Types are computed in a bottom-up pass over the AST

---

# Rules for Variables

* What is the type of a variable reference?

<center>
x is a variable 
⊢ x: ?
</center>

* The local rule doesn't carry enough information to give `x` a type

* We need more information from somewhere

---

# Type Environments

A _type environment_ gives types for _free_ variables

* The type of an identifier can be looked up in the _type environment_, like the `find_symbol()` operation on a symbol table

* A variable is _free_ in an expression if it is not declared within the expression

* S ⊢ E: T means "assuming that variables have types given by S (the type environment), it is provable that the expression E has the type T"

* S[T/x] means "S is modified to set the type T for the identifier x"

---

# Rules for Variables

* The type of a variable reference is looked up in the type environment:

* The type of a variable declaration sets the type environment:

---

# Type Environment

* The type environment sets types for the free identifiers in the current scope

* The type environment is passed down the AST from the root towards the leaves (parent to child)

* Types are computed up the AST from the leaves towards the root (child to parent)

---

# Rules for Assignment

* The type of the variable x must be compatible with the type of the value assigned to it:

---

# One-Pass Type Checking

* Type checking can be implemented in a single traversal over the AST
  * Type environment passed down the tree
  * Types passed up the tree

Example:
<center>
S ⊢ E1: int &nbsp;&nbsp; S ⊢ E2: int 
S ⊢ E1 + E2: int
</center>

Informal pseudo-code:

_TypeCheck(Environment, E1 + E2) {_

> _T1 = TypeCheck(Environment, E1)_ 
> _T2 = TypeCheck(Environment, E2)_ 
> _verify T1 == T2 == int_ 
> _return int_

_}_